Varians
Dalam teori probabilitas dan statistika, varians (dari bahasa Inggris: variance) atau ragam suatu perubah acak (atau distribusi probabilitas) adalah ukuran bagi persebaran (dispersi) data. Yang diukur adalah seberapa jauh data tersebar di sekitar rerata). Varians merupakan salah satu parameter bagi distribusi normal. Akar dari varians dikenal sebagai simpangan baku (standard deviation). Istilahvarians pertama kali diperkenalkan oleh Fisher dalam makalahnya pada tahun 1918 yang berjudul The Correlation Between Relatives on the Supposition of Mendelian Inheritance ("Korelasi di Antara Kerabat dalam Kerangka Pewarisan Mendel").
Rata-rata dari jumlah nilai simpangan dikenal dengan
ragam(
varians). Setelah nilai ragam diperoleh, selanjutnya nilai ragam tersebut diakarkan untuk mendapatkan kembali satuan asal dari variabel tersebut (
bukan kg2/petak2, tapi kg/petak 
) . Cara pengukuran keragaman seperti ini dikenal dengan
Standar deviasi.
Secara matematis, standar deviasi dapat dihitung dengan menggunakan formula:
Standar deviasi populasi disimbolkan dengan ? (baca ‘sigma’) dan standar deviasi sampel disimbolkan dengans. Standar deviasi sampel yang baik seharusnya merupakan ukuran yang tidak bias terhadap standar deviasi populasinya, karena kita menggunakan ukuran standar deviasi sampel untuk memperkirakan nilai standar deviasi populasi. Untuk itu, nilai n pada formula di atas diganti dengan n – 1 sehingga formula untuk standar deviasi sampel adalah sebagai berikut:
Mengapa harus diganti dengan
n-1?! Pembuktiannya diluar bahasan blog ini.

Data pada tabel distribusi frekuensi:
Data Tunggal:
Data kelompok (sudah digrupkan berdasarkan selang tertentu):
Sama seperti pada perhitungan simpangan rata-rata. Standar deviasi dan ragam yang dihitung dari distribusi frekuensi data yang sudah dikelompokkan menggunakan nilai data perkiraan, bukan data aslinya. Data pewakil tersebut disimbolkan dengan m. Untuk membuat perhitungan dari data yang sudah dikelompokkan kita harus menganggap, bahwa semua nilai dalam sebuah kelas, sama dengan nilai pewakilnya (tanda kelasnya, mi). Selanjutnya, nilai perkiraan standar deviasi dapat dihitung dengan menggunakan rumus:
Nilai kuadrat dari standar deviasi dikenal dengan ragam (
variance). Pada teknik
analisis varian,
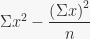
dikenal dengan
Jumlah Kuadrat (
Sum of Square), dan
ragam (
varian) dikenal dengan istilah
Kuadrat Tengah/Rata-rata Jumlah Kuadrat (
Mean Square).
Standar deviasi merupakan ukuran penyebaran yang paling banyak digunakan. Semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi, sama halnya seperti mean.
Standar Deviasi memiliki beberapa karakteristik khusus lainnya. SD tidak berubah apabila setiap unsur pada gugus datanya di tambahkan atau dikurangkan dengan nilai konstan tertentu. SD berubah apabila setiap unsur pada gugus datanya dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali dari nilai standar deviasi aktual dengan konstan.
Contoh 6
Apabila data nilai Quiz pada contoh 2 diambil dari sampel, tentukan nilai ragam dan standar deviasinya.
Jawab:
Untuk mencari nilai standar deviasi sampel, kita bisa menggunakan salah satu formula berikut:
Formula pertama adalah formula secara definitif. Formula yang direkomendasikan untuk perhitungan secara manual adalah formula yang ke-2. Cara perhitungan dengan formula yang ke-2 bisa di lihat pada contoh 7 dan 8. Pada contoh ini, sebagai latihan, kita gunakan formula yang pertama. Untuk perhitungan dengan formula pertama, kita memerlukan nilai rata-ratanya, sehingga terlebih dahulu kita harus menghitung nilai rata-ratanya.
Quiz I: rata-rata =18.27
Quiz 2: rata-rata = 10.82
| No | Quiz 1(xi) | 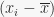 | 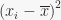 | | Quiz 2(xi) | 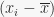 |  |
| 1 | 1 | -17.27 | 298.35 | | 2 | -8.82 | 77.76 |
| 2 | 20 | 1.73 | 2.98 | | 3 | -7.82 | 61.12 |
| 3 | 20 | 1.73 | 2.98 | | 4 | -6.82 | 46.49 |
| 4 | 20 | 1.73 | 2.98 | | 5 | -5.82 | 33.85 |
| 5 | 20 | 1.73 | 2.98 | | 6 | -4.82 | 23.21 |
| 6 | 20 | 1.73 | 2.98 | | 14 | 3.18 | 10.12 |
| 7 | 20 | 1.73 | 2.98 | | 15 | 4.18 | 17.49 |
| 8 | 20 | 1.73 | 2.98 | | 16 | 5.18 | 26.85 |
| 9 | 20 | 1.73 | 2.98 | | 17 | 6.18 | 38.21 |
| 10 | 20 | 1.73 | 2.98 | | 18 | 7.18 | 51.58 |
| 11 | 20 | 1.73 | 2.98 | | 19 | 8.18 | 66.94 |
| | Jumlah | 328.1818 | | | | 453.6364 |
Quiz 1:
Quiz 2:
Kesimpulan:
Berdasarkan nilai ragam dan standar deviasi, Quiz ke-2 lebih bervariasi dibandingkan dengan Quiz ke-1. (kesimpulannya berbeda dengan kesimpulan berdasarkan range)
Contoh 7
Hitung nilai standar deviasi dan ragam dari tabel frekuensi data tunggal berikut:
| No | xi | fi |
| 1 | 70 | 5 |
| 2 | 69 | 6 |
| 3 | 45 | 3 |
| 4 | 80 | 1 |
| 5 | 56 | 1 |
| Jumlah | 320 | 16 |
Jawab:
Untuk kemudahan dalam perhitungan secara manual, kita gunakan formula standar deviasi berikut:
Selanjutnya kita buat tabel seperti pada tabel berikut:
| No | xi | fi | fi.xi | fi.xi2 |
| 1 | 70 | 5 | 350 | 24500 |
| 2 | 69 | 6 | 414 | 28566 |
| 3 | 45 | 3 | 135 | 6075 |
| 4 | 80 | 1 | 80 | 6400 |
| 5 | 56 | 1 | 56 | 3136 |
| Jumlah | 320 | 16 | 1035 | 68677 |
Dari tabel tersebut didapat:
n = 16
mean = 1035/12 = 64.69
Standar deviasi:
Contoh 8
Hitung nilai standar deviasi dan ragam dari tabel frekuensi yang sudah dikelompokkan:
Tabel berikut ini adalah nilai ujian statistik 80 mahasiswa yang sudah disusun dalam tabel frekuensi. Berbeda dengan contoh di atas, pada contoh ini, tabel distribusi frekuensi dibuat dari data yang sudah dikelompokkan berdasarkan selang/kelas tertentu (banyak kelas = 7 dan panjang kelas = 10).
| Kelas ke- | Nilai Ujian | fi |
| 1 | 31 – 40 | 2 |
| 2 | 41 – 50 | 3 |
| 3 | 51 – 60 | 5 |
| 4 | 61 – 70 | 13 |
| 5 | 71 – 80 | 24 |
| 6 | 81 – 90 | 21 |
| 7 | 91 – 100 | 12 |
| Jumlah | 80 |
Jawab:
Untuk kemudahan dalam perhitungan secara manual, kita gunakan formula standar deviasi berikut:
Selanjutnya kita buat daftar tabel berikut, tentukan nilai tengah kelas/pewakilnya (mi) dan lengkapi kolom berikutnya.
| Kelas ke- | Nilai Ujian | fi | mi | fi.mi | fi.mi2 |
| 1 | 31 – 40 | 2 | 35.5 | 71.0 | 2520.5 |
| 2 | 41 – 50 | 3 | 45.5 | 136.5 | 6210.8 |
| 3 | 51 – 60 | 5 | 55.5 | 277.5 | 15401.3 |
| 4 | 61 – 70 | 13 | 65.5 | 851.5 | 55773.3 |
| 5 | 71 – 80 | 24 | 75.5 | 1812.0 | 136806.0 |
| 6 | 81 – 90 | 21 | 85.5 | 1795.5 | 153515.3 |
| 7 | 91 – 100 | 12 | 95.5 | 1146.0 | 109443.0 |
| Jumlah | 80 | 458.5 | 6090.0 | 479670.0 |
Dari tabel tersebut didapat:
n = 80
mean = 6090/80 = 76.13
Standar deviasi dan ragam:
Contoh Tambahan:
Dengan cara yang sama seperti di atas, nilai standar deviasi untuk ketiga varietas:
Varietas I = 1.87
Varietas II = 9.49
Varietas III = 2.35
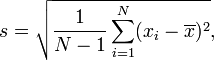
 adalah nilai data dari sampel dan
adalah nilai data dari sampel dan  adalah rata-rata dari sampel.
adalah rata-rata dari sampel.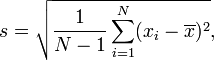
 adalah nilai data dari sampel dan
adalah nilai data dari sampel dan  adalah rata-rata dari sampel.
adalah rata-rata dari sampel.









